シミュレーション

Ginibre点過程とPoisson点過程

2次元空間の典型的な点過程である、Ginibre点過程とPoisson点過程のシミュレーションは以下のとおりです。

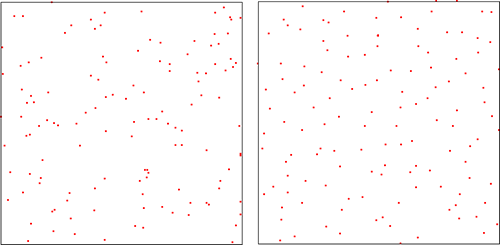
左がPoisson点過程、右がGinibre点過程です。これらは、共に平行移動不変かつ回転不変です。Poisson点過程は、いわば配置空間の世界の最も標準的な測度、つまり、「Lebesgue測度」の役割を果たすもので、シミュレーションのように、粒子は大変ランダムに散らばります。一方、Ginibre点過程は、対数ポテンシャル（2次元クーロンポテンシャル）で、互いに反発力を受けます。長距離の大変強い相互作用を持ちますから、その性質は、PoissonやGibbs測度と異なります。最近その研究が、Peres-Ghosh、Bufetov、Osada-Shiraiなどによって、盛んに研究されています。ある種、結晶構造に近い、「幾何的剛性」をGinibre点過程が持っています。本研究で、これらの結果は、確率力学の性質に受け継がれ、鮮やかに反映されることが分かってきました。

Ginibre干渉ブラウン運動のシミュレーション

解説と、確率微分方程式の形は、前研究のホームページを参照して下さい。
http://www2.math.kyushu-u.ac.jp/~osada/racing.html
http://www2.math.kyushu-u.ac.jp/~osada/outline.html
以前の研究に関するホームページに、信州大学の乙部さんが作成したシミュレーションに関するリンクを張りましたが、ここでは、新たにBenSaid君が作成したシミュレーションをお見せします。

有限粒子系のシミュレーションを行った場合、中心力がある場合と、無い場合の二通りが考えられます。下記でscheme1は、中心力がある場合、scheme2は無い場合です。粒子数無限大に於いては、scheme1であっても、中心力が無限個の粒子相互の反発力で相殺され中心力のない平行移動不変な無限粒子系の挙動に収束します。粒子数を増やすと、その様子が手に取るようにわかります。
　一般に逆温度βが大きいと粒子の相互作用の影響が強くなります。この時、βを無限大に近づけていくと、Scheme1においては、粒子全体が円をなすことが分かります。

粒子数Nと逆温度βの値を様々にとっています。このシミュレーションからは、低温極限で3角格子なる事が見て取れます。

(scheme1)

(scheme 2)

原点の近くを観測しています。最初多くの粒子を原点近くから出発させたため、反発力のため粒子は飛び散りますが、粒子数が多いので、少し時間がたつと漸次安定します。しばらくの間は、漸近的に定常な状態になります。
http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-29-sheme2-1000-zoom/scheme2.html
大きなβ=1000、多数の粒子N=5000で原点近くを観測します。
http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-7-N=1000-noOU/scheme2.html
http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-7-N=1000-noOU/zoom-near-origin-beta=5000.html
小さなβ=0.5と1.0、多くの粒子N=5000で原点近くを観測します。3角格子は現れません。つまり、相転移が予想されます。
http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-11-N=5000-noOU-small-beta/scale-example.html

Ginibre点過程とPoisson点過程
Ginibre干渉ブラウン運動のシミュレーション