Ginibre干渉ブラウン運動の動画

　N個の粒子からなるGinibre干渉ブラウン運動のシュミレーションが研究協力者の乙部厳己氏によって制作されました．その動画を，紹介します.
http://www2.math.kyushu-u.ac.jp/~osada/otobe/simulation.html
次に、モデルを表す確率微分方程式について説明します．

シュミレーションの説明：

Nを粒子の個数とします．粒子の運動を表す確率微分方程式(SDE)は，

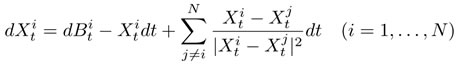
となります．前述の無限粒子系のGinibre を表すSDE は(β = 2 のとき)

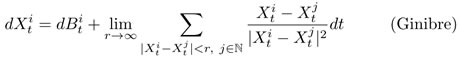
となります．一見，有限系に比べて中心力が働かなくなっているように見えますが，実はこのSDE は，第二の表現を持ちます．

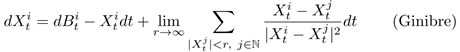
ここで無限和は条件収束であり，この二つのSDEは、Ginibre点過程について確率１の初期条件に対して同一の無限次元拡散過程を定義します．もし初期条件が有限個の粒子からなる場合は、明らかに違うSDEでありそれが定める確率過程も異ります。このようなSDE表現の多様性は，無限系およびCoulombポテンシャル特有の現象です．後者の表現は，シュミレーションの有限粒子系の形に対応しています．動画ではGinibre と独立なOrnstein-Uhlenbeck過程を考え比較することにより，Coulombポテンシャルの強烈な効果が実感できます． 粒子数に応じて尺度が違いますが，N = 800になるとOrnstein-Uhlenbeck過程は,ほぼ点のように見えます．しかしGinibre干渉ブラウン運動は，Coulombポテンシャルの反発力で，特に中心部は平行移動不変な状態になっており、全体としてボールのような形を形成する確率力学となります．