​Simulation

The Ginibre RPFs and the Poisson RPFs

Simulations of the Ginibre random point fields(RPFs) and the Poisson RPFs, which are typical RPFs in two-dimensions, are as follows.

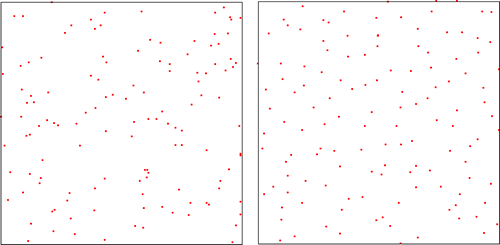
The left-hand side is the Poisson RPFs, while the right-hand side is the Ginibre RPFs. Both of them are translation and rotation invariant in space. The Poisson RPFs is the most standard measure in the configration space, namely, that serves a function of the Lebesgue measure in the Euclidean space. Particles of the Poisson RPFs are very randomly scattered as shown above. On the other hand, these of Ginibre RPFs recieve repulsive force with logarithmic potentials (two-dimensional Coulomb potentials) from each others. This property of the Ginibre RPFs is different from that of the Poisson RPFs and the Gibbs measure because of a long-distance strong interaction. Recently this research has been actively conducted by Peres--Ghosh, Bufetov and Osada--Shirai, etc. The Ginibre RPFs has "geometric stiffness" close to a crystal structure in a sense. It has elucidated that these results are inherited to the property of stochastic dynamics and reflected vividly.

Simulations of the Ginibre interacting Brownian motion

Please refer to the website of previous research for explanation and the form of stochastic differntial equations (Japanese only).
http://www2.math.kyushu-u.ac.jp/~osada/racing.html
http://www2.math.kyushu-u.ac.jp/~osada/outline.html

There are simulational movies created by related investigator Yoshiki Otobe (Shinshu University) on the link above. We show another simulations newly created by Mr. BenSaid here.

There are two patterns in case of simulation of Finite Particle Systems. Scheme 1 below is when there is a central force, scheme 2 is nothing. In infinite particles, even in scheme 1, it converges to the behavoir of transition invariant infinite particle systems with no central force because the central force is canceled out by the repulsive force between the infinite number of particles. As the number of particles increases, you can see how it looks like.

Generally, the larger the reverse temperature β, the stronger an influence of the interaction among particles. At this time, as β approaches infinity, it turns out that the whole particle forms a circle in scheme 1.

We take various values of particle number N and inverse temperature β. You can see that it becomes a triangular lattice at the low temperature limit from this simulation.

(scheme1)

1. http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-28,1,2,4,1000/beta=0,2.html
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-28,1,2,4,1000/beta=1.html
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-28,1,2,4,1000/beta=2.html
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-28,1,2,4,1000/beta=2.html
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-28,1,2,4,1000/beta=4.html
2. In case β is extreamly large.
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-1beta=3000-4000/extreme values.html

(scheme 2)

1. We observe near the origin. Particles are scattered because of the repulsive force, but since the number of particles is large, it gradually stabilizes as time goes on for a while.
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/5-29-sheme2-1000-zoom/scheme2.html
2. Observing near the origin with large β = 1000 and numerous particles N = 5000
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-7-N=1000-noOU/scheme2.html
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-7-N=1000-noOU/zoom-near-origin-beta=5000.html
3. Observing near the origin with small β = 0.5 and 1.0, and numerous particles N = 5000
   A triangular lattice does not appear. That is, a phase transition is expected.
   http://www2.math.kyushu-u.ac.jp/~osada/public-2_html/Simulation/6-11-N=5000-noOU-small-beta/scale-example.html

• The Ginibre RPFs and the Poisson RPFs
• Simulation of the Ginibre interacting Brownian motion