問１. 上に有界な 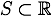が最大数を持つためには 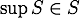が必要十分であること。

ほとんどの人が「明らか」などとして説明できていないようでしたので、○×は付けていません。現象を正確に理解して、さらに正確に言葉で表現するのは難しいのです。

[解答]

必要性： が最大数 を持つとする。定義から任意の に対して だから は の上界である。一方どんな も より小さいから の上界にはなり得ない。以上から は の上限である。よって である。

十分性： のとき、 は の最大数である。

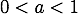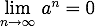問３. のとき を示せ。

なぜか、簡単なこちらの方ができていませんでした。多かった間違いは a が 1 より大きい場合の結果に定理 1 を使って などとしたものです。∞ は数ではありませんから、このような書き方はできません。また a_n, b_n のいずれかが発散する場合には定理１は使えませんので気をつけてください。代わりに問２の (1) を使います。

[解答]

仮定から , () と書ける。このとき問２の (1) から

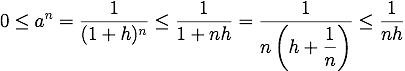
が成り立つ。この一番左と右はともに 0 に収束するから、挟み撃ちの原理により主張が従う。

余談ですが、「題意を満たす。」というのは某受験数学雑誌の編集者が造り出した表現で、日本語としては滑稽です。