Time Table
PDF File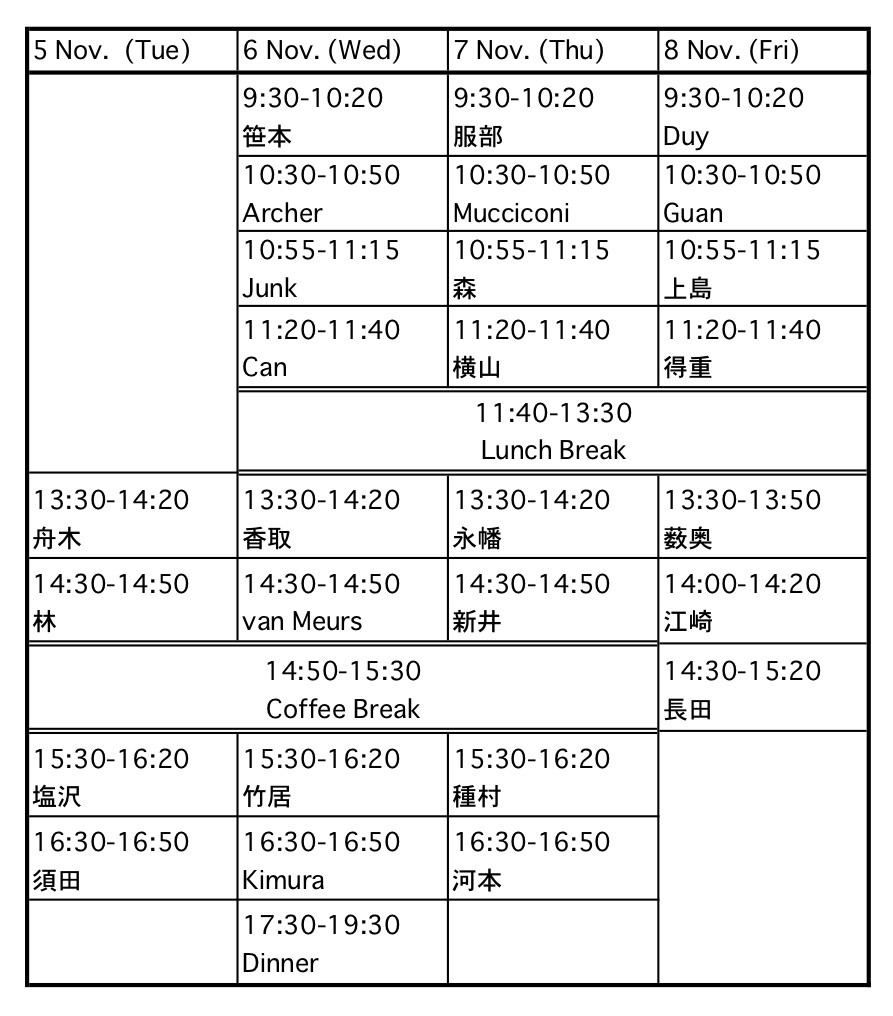
Titles and Abstracts
Please click a title to read an abstract.
5 Nov. (Tue.)
- 13:30 - 14:20 Tadahisa Funaki (Waseda University)
- 14:30 - 14:50 Kohei Hayashi (University of Tokyo)
- 15:30 - 16:10 Yuichi Shiozawa (Osaka University)
- 16:30 - 16:50 Hayate Suda (University of Tokyo)
We first briefly recall the result on the coupled KPZ equation with M. Hoshino (JFA, '17) based on the paracontrolled calculus. Then, we discuss scaling limits of the empirical mass fluctuation fields of weakly asymmetric multi-species zero-range processes on a one-dimensional discrete torus starting from stationary initial conditions. In a certain characteristic frame of reference we derive coupled KPZ-Burgers systems. We rely on the notion of energy solutions studied recently by Gubinelli and Perkowski. This is joint work with C. Bernardin and S. Sethuraman, and on arXiv:1908.07863.
We consider Glauber-Kawasaki type dynamics with two components under strong competition. As the scaling parameter tends to infinity, assuming that the reaction rate diverges, territories of two species are spatially segregated and an interface governed by a free boundary problem appears. Recently, DeMasi, Funaki, Presutti and Vares derived the free boundary problem directly from the Glauber-Kawasaki dynamics when two species has the same strength to compete with each other. In this talk, we focus on the case where competition dynamics between two species is “unbalanced”, namely, one kind of particles has a stronger effect to kill the other kind of particles. Further assuming the diffusion coefficient of one type of particles is zero, we derive three kinds of limiting interfaces: Vanishing, moving and immovable interfaces as a hydrodynamic limit of our microscopic systems with several types of competitive reaction.
In this talk, we are concerned with the forefront of particles for a branching Brownian motion with spatially inhomogeneous structure. We first reveal the growth rate of the population outside balls with time dependent radius. This implies the linear growth rate of the forefront. We next study the fluctuation and tail probability of the upper deviation type for the forefront. We finally show the existence of the Yaglom type limit on the population outside the forefront. The latter two parts are based on a joint work with Yasuhito Nishimori (National Institute of Technology, Anan College, Japan).
In this talk, we consider one-dimensional infinite chains of harmonic oscillators with stochastic perturbation and long-range interactions which have polynomial decay rate $|x|^{-\theta }$, $\theta > 1$ where $x \in \mathbb{Z}$ is the interaction range. Since our stochastic perturbation is conservative, the system has three conserved quantities : momentum, generalized tension, and energy. We show that if $\theta \le 3$ then the long-range effect appears macroscopically, and there exist two different space-time scaling and the corresponding macroscopic time evolution equations of the conserved quantities. On the scales space : time $ = \epsilon $ : $\epsilon^{\frac{\theta - 1}{2}}$, $1< \theta < 3$ the limits of the conserved quantities satisfies superballistic wave equations, that is, the momentum $p(y,t)$ satisfies $\partial_t^2 p(y,t) = -(-\Delta)^\frac{\theta - 1}{2} p(y,t)$. On the scales space : time $ = \epsilon : \epsilon^{\frac{6}{7-\theta}}, 2 < \theta < 3$, the macroscopic thermal energy evolves according to a fractional diffusion equation with the exponent $\frac{3}{7 - \theta}$.
6 Nov. (Wed.)
- 9:30 - 10:20 Tomohiro Sasamoto (Tokyo Institute of Technology)
- 10:30 - 10:50 Eleanor Archer (Kyoto University & University of Warwick)
- 10:55 - 11:15 Stefan Junk (Kyoto University)
- 11:20 - 11:40 Van Hao Can (Kyoto University & Vietnam Academy of Science and Technology)
- 13:30 - 14:20 Makoto Katori (Chuo University)
- 14:30 - 14:50 Patrick van Meurs (Kanazawa University)
- 15:30 - 16:20 Masato Takei (Yokohama National University)
- 16:30 - 16:50 Bruno Kimura (Hokkaido University)
Since the work by Johansson in 2000 for the totally asymmetric
simple exclusion process (TASEP), many works have shown that
the limiting current fluctuations of various stochastic interacting
particle systems are given by the Tracy-Widom (TW) type distributions,
widening the applicability of the Kardar-Parisi-Zhang (KPZ) universality
class. However, most results so far have been restricted to single component
models.
In this presentation we consider a two-species asymmetric exclusion process,
known as the Arndt-Heinzel-Rittenberg (AHR) model, in which two species of
particles stochastically hop in the opposite directions and swap their positions
when they meet. We first construct the transition probability by applying the
Bethe ansatz. From this we obtain a multiple integral formula for a certain current fluctuation and show that in the scaling limit it tends to the product of a GUE TW and a Gaussian. Our work is also considered as the first microscopic confirmation of the nonlinear fluctuating hydrodynamics proposed by H. van Beijeren and H. Spohn [1].
This is based on a joint work with Z. Chen, J. de Gier and I. Hiki [2].
[1]H. Spohn, Nonlinear Fluctuating Hydrodynamics for Anharmonic Chains,
J.Stat. Phys. 154 (2014) 1191.
[2]Z. Chen, J. de Gier, I. Hiki, T. Sasamoto,
Exact confirmation of 1D nonlinear fluctuating hydrodynamics
for a two-species exclusion process, Phys. Rev. Lett. 120, 240601 (2018)
(arXiv:1803.06829). A longer version is in preparation.
Random looptrees are a class of objects that arise naturally in the study of statistical mechanics models on random planar maps, and are used to describe the structures of discrete graphs that are "tree-like" but constrained to have large faces. In this talk I will introduce random walks on looptrees, give an invariance principle, and discuss properties of the limiting diffusion. Time permitting, I will also discuss applications to some other planar map models.
In the Brownian polymer model, introduced by Comets and Yoshida, we consider Brownian motion in the presence of a random (Poissonian) set of space-time obstacles. An important quantity is the exponential decay rate of the survival probability, which is called the free energy. At positive temperature (soft obstacles) the existence of the free energy follows from standard super-additivity and concentration arguments, but due to an integrability issue this technique does not work in the zero temperature (hard obstacle) case. We show existence and continuity of the free energy in zero temperature. Joint work with Ryoki Fukushima (Kyoto University).
In this talk, we consider Glauber dynamics of Ising model on random regular graphs in both annealed and quenched settings. We discuss on the phase transition of the mixing time when the parameters cross the critical values. We also show that the annealed dynamics mixes faster than the quenched one in sufficiently low temperature regime. Based on a joint work with Remco van der Hofstad and Takashi Kumagai.
Peres and Virág studied the i.i.d. Gaussian power series in the unit disk $\mathbb{D}$ whose covariance kernel is given by the Szegö kernel of $\mathbb{D}$. They proved that the zero set of this Gaussian analytic function (GAF) is a determinantal point process whose correlation kernel is given by the Bergman kernel of $\mathbb{D}$. We consider a family of i.i.d. Gaussian Laurent series in the annulus $\mathbb{A}_q :=\{z \in \mathbb{C} : q < |z| < 1\}$ with $0 < q < 1$ whose covariance kernels are given by extensions of the Szegö kernel of $\mathbb{A}_q$ with a parameter $t$ satisfying $q^2 < t < 1$. We will characterize the point processes of zeros of this two-parameter $(q, t)$ family of GAFs in $\mathbb{A}_q$. This talk is based on the joint work with Tomoyuki Shirai (IMI, Kyushu University).
We consider $n$ many particles on a periodic lattice with spacing $d$. The dynamics of the particles is given by a random walk with drift. The drift is given by the interaction force exerted by all other particles. Our interest is not just in passing to the limit as both $n$ tends to infinity and $d$ tends to 0, but also in deriving convergence rates for this convergence. For the limit $n$ to infinity we obtain such a convergence rate by proving propagation of chaos, and for the limit $d$ to 0 we rely on tools from numerical analysis to to establish a bound on the difference between the laws of the related processes.
This is joint work with T. Hudson (University of Warwick) and M. A. Peletier (Eindhoven University of Technology).
We study the limiting behavior of edge-reinforced random walks on the half-line with heterogeneous initial weights. Takeshima (2001) proved that the initial transience is preserved under reinforcement. For linear reinforcement, Takeshima (2000) showed that the initial recurrence is also preserved. We give new proofs of those facts. On the other hand, the result of Davis (1989) shows that the initial recurrence is not necessarily preserved under reinforcement. We consider the situation where each edge weight can be updated only when the edge is traversed from right to left, and provide a description of phase transitions that arise as trade-offs between the strength of the reinforcement and that of the initial weights. The latter part is based on a joint work with Jiro Akahori and Andrea Collevecchio.
The rigorous study of metastability in the setting of stochastic dynamics is a relatively recent topic.
One of the most interesting problems that have been investigated is the study of the dependence
on the dynamics of metastable behavior and nucleation towards the stable phase . Such class
of problems appears in the literature considering several dynamic regimes, however, in most of them
the microscopic interactions are assumed to be of shot range.
Therefore, the following questions naturally arise: Does indeed a long range interaction
change substantially the nucleation process? Are we able to define in this framework a critical configuration
triggering the crossover towards the stable phase?
In this talk I will show that under very general assumptions, the 1D long range Ising model with
a weak uniform field (without loss can be assumed to be positive) evolving according to the Metropolis dynamics,
the state ${\bf -1}$ is a metastable configuration that nucleates toward the stable phase ${\bf +1}$. It is possible to determine the tunneling time and the critical configurations that triggers the nucleation. Some model-dependent examples and generalizations are also discussed.
7 Nov. (Thu.)
- 9:30 - 10:20 Tetsuya Hattori (Keio University)
- 10:30 - 10:50 Matteo Mucciconi (Tokyo Institute of Technology)
- 10:55 - 11:15 Takahiro Mori (Kyoto University)
- 11:20 - 11:40 Satoshi Yokoyama (Waseda University)
- 13:30 - 14:20 Yukio Nagahata (Niigata University)
- 14:30 - 14:50 Yuta Arai (Chiba University)
- 15:30 - 16:20 Hideki Tanemura (Keio University)
- 16:30 - 16:50 Yosuke Kawamoto (Fukuoka Dental College)
We prove a hydrodynamic limit of stochastic ranking processes (SRP) with position dependent intensities, systems of particles aligned in a line with move-to-front rules driven by point processes, allowing dependence of intensity functions of the driving processes on positon variables, which implies non-trivial stochastic dependence among the particles. For a proof, we introduce an intermediate model which is driven by what we name `the point processes with last-arrival-time dependent intensities', which, unlike Poission processes, lack independence of disjoint increments. In fact, the hydrodynamic limit corresponds to the solution to a system of partial differential equations of one-dimensional fluid solved by characteristic curves, generalized to allow for non-local interaction terms whose solutions are found to be written by the expectations of the above introduced processes.
A number of processes of interest in the realm of Integrable Probability can be described as marginal Markov projections of more general dynamics on interlacing arrays. This structure was first discovered by Sasamoto in 2005 and later extended in a number of papers culminating with the introduction of the Macdonald Processes by Borodin and Corwin. Models that fall into this scheme include TASEP, PNG, certain random matrix ensembles and then $q$-TASEP, log-Gamma polymers and the KPZ equation itself. More recently a generalization of the models listed above came in the form of $sl_2$ stochastic vertex models. Among these we have, for example the Higher Spin Six Vertex Model and the $q$-Hahn TASEP, often seen as a discrete generalization of a model of random walkers in a Beta-random environment (RWRE). A question that was asked a number of times in literature was to inscribe the theory of $sl_2$ stochastic vertex models (especially in the case of RWRE) into that of Macdonald-like processes. In the presentation I will explain how this is done by introducing suitable deformations of Macdonald functions.
The talk is based on collaborations with A.Bufetov and L.Petrov.
For several independent (possibly different) stochastic processes on the same state space, consider the intersection measure of the processes, which is intuitively regarded as the occupation measure of intersections of the processes.
W. König and C. Mukherjee (2013) showed a Donsker-Varadhan type large deviation principle for the normalized intersection measure in the case of Brownian motions before exiting some bounded open set.
X. Chen and J. Rosen (2005) showed exponential asymptotics of the intersection measure in the case of Brownian motions or stable processes.
In this talk, we discuss some extensions of these facts via Dirichlet form techniques.
In [1], we studied the sharp interface limit for
stochastically perturbed mass-conserving Allen-Cahn equation.
The reaction term is bistable and satisfies the balance condition.
The initial value was assumed to be close to one of the two stable values, and stochastic
volume-conserving motion by mean curvature was derived in the limit.
In this talk, we consider general initial values.
Before reaching the stage discussed in [1], the dynamics
undergoes two different time stages in much shorter time span.
The first is an ODE stage and then the second is Huygens stage.
This is joint work with Dimitra Antonopoulou, Tadahisa Funaki and Georgia Karali.
[1]T. FUNAKI AND S. YOKOYAMA, ${\it Sharp~ interface~ limit~ for~ stochastically ~perturbed~ mass~ conserving}$
${\it ~Allen-Cahn~ equation},~ Ann.~ Probab.,~ {\bf 47}~ (2019)~ 560--612.$
A stochastic ranking process is driven according to an algorithm for self-organizing linear list of finite number of items.
T.Hattori proved the hyperbolic scaling limit of the tagged particles dynamics and the joint empirical distribution of jump rate and position of particles.
By using these results, we give a diffusive scaling limit of the tagged particle dynamics.
The totally asymmetric simple exclusion process (TASEP) is one of the simplest interacting stochastic particle system and can be interpreted as a stochastic growth model of an interface, which turns out to belong to the Kardar-Parisi-Zhang (KPZ) universality class.
In this talk we consider a discrete time version of the TASEP with arbitrary right
finite initial condition. We obtain a single Fredholm determinant representation
for the joint distribution function of particle positions.
Using this, we show that in the KPZ 1:2:3 scaling limit,
the distribution function converges to the one describing the KPZ fixed point
introduced in [1].
[1] Konstantin Matetski, Jeremy Quastel, Daniel Remenik, The KPZ fixed point. arXiv:1701.00018.
Ben-Ari and Schinazi (2016) introduced a stochastic model to study `virus-like evolving population with high mutation rate'. This model is a birth and death model with an individual at birth being either a mutant with a random fitness parameter in $[0,1]$ or having one of the existing fitness parameters with uniform probability; whereas a death event removes the entire population of the least fit site. We change this to incorporate the notion of `survival of the fittest', by requiring that a non-mutant individual, at birth, has a fitness according to a preferential attachment mechanism, i.e., it has a fitness $f$ with a probability proportional to the size of the population of fitness $f$. Also death just removes one individual at the least fit site. This preferential attachment rule leads to a power law behaviour in the asymptotics, unlike the exponential behaviour obtained by Ben-Ari and Schinazi (2016).
For random point fields with infinitely many particles, we
consider Dirichlet forms to construct and analyse equilibrium dynamics.
There are two typical Dirichlet forms, that is, the upper Dirichlet form
and the lower Dirichlet form.
A difference of these two is these domains and the domain of the lower
Dirichlet form contains that of the upper one.
Then the natural problem of uniqueness of Dirichlet forms arises: when
the domains are the same and the two Dirichlet forms correspond?
A sufficient condition of the uniqueness of Dirichlet forms is known.
The essential conditions of this are the following three: non-explosion
of tagged particles of the equilibrium dynamics, infinite-dimensional
stochastic differential equation representation of the dynamics, and the
tail triviality of a random point field.
In these, the most difficult condition to check is the tail triviality.
For example, the first two conditions have been shown for Airy random
point fields for the inverse temperature $\beta $=1,2,4, but the tail
triviality has been proven only for $\beta $=2.
In this talk, I will give a sufficient condition of the uniqueness of
Dirichlet forms WITHOUT using the tail triviality.
8 Nov. (Fri.)
- 9:30 - 10:20 Trinh Khanh Duy (Waseda University)
- 10:30 - 10:50 Zehao Guan (University of Tokyo)
- 10:55 - 11:15 Yoshinori Kamijima (Hokkaido University)
- 11:20 - 11:40 Yuki Tokushige (Kyoto University)
- 13:30 - 13:50 Satoshi Yabuoku (Chiba University)
- 14:00 - 14:20 Syota Esaki (Fukuoka University)
- 14:30 - 15:20 Hirofumi Osada (Kyushu University)
Beta ensembles on the real line are known as the equilibrium measure of a one dimensional Coulomb log-gas under an external potential $V$ at the inverse temperature $\beta $. The ensembles have been studied extensively in case the parameter $\beta $ is fixed. This talk, however, introduces the study of the beta ensembles in a high temperature regime, a regime where the temperature is proportional to the system size. In this regime, a large deviation principle has been studied recently. Consequently, the empirical distribution converges weakly to a full-supported measure. Looking at local behaviors around any fixed point, we will show that the local statistics converges weakly to a homogeneous Poisson process. The result is universality in the sense that it holds for a wide class of potentials $V$. This is based on the joint work with Prof. F. Nakano (Gakushuin University).
We study the hydrodynamic limits of the simple exclusion processes and the zero range processes on crystal lattices. For a periodic realization of crystal lattice, we derive the hydrodynamic limit for the exclusion processes and the zero range processes, which depends on both the structure of crystal lattice and the periodic realization. Even through the crystal lattices have inhomogeneous local structure, for all periodic realizations, we apply the entropy method to derive the hydrodynamic limits. Also, we discuss how the limit equation depends on the choices of the realizations.
We will consider a critical behavior of the susceptibility $\chi(\beta)$ with respect to the inverse temperature $\beta$ for the quantum Ising ferromagnet. As a first step, we followed the established way for the classical Ising model $[M.~Aizenman,~ {Commun. Math. Phys.}~ \textbf{86},~ 1982]$ and derived an inequalities for $\chi(\beta)$ via the Suzuki-Trotter transformation (see, e.g., $[K.,~ RIMS~ Kôkyûroku~ \textbf{2116},~ 2019]$ or $[S. Handa, Ph.D. thesis, 2019]$). At that time, however, we had used the monotonicity for $\chi(\beta)$ with respect to $\beta$ with an extra condition. Our next aim is to drop such condition and show the infrared bound for the quantum Ising model.
In this talk, I will show some attempts to prove the critical behavior via another way: the graphical representation in terms of the space-time Ising model which originates from $[J.E.~Björnberg~ and~ G.R.~Grimmett,~$ $\textit{J. Stat. Phys.}~\textbf{136},~ 2009]$. This is based on a joint work with Satoshi Handa (Fujitsu Laboratories Ltd.) and Akira Sakai (Hokkaido University).
We prove that the speed of a $\lambda$-biased random walk on a supercritical Galton-Watson tree is differentiable for $\lambda$ such that the walk is ballistic and obeys a central limit theorem, and give an expression of the derivative using a certain 2-dimensional Gaussian random variable.
The proof heavily uses the renewal structure of Galton-Watson trees that was introduced by Lyons-Pemantle-Peres.
This talk is based on the joint work with Adam Bowditch (National University of Singapore).
We consider the eigenvalue process of elliptic Ginibre ensemble. In random matrix theory, elliptic Ginibre ensemble is the interpolation between GUE(Gaussian Unitary ensemble) and Ginibre ensemble. GUE is hermitian and Ginibre ensemble has no symmetry. The eigenvalue process of GUE is well known as Dyson’s model and recently the dynamical model of Ginibre ensemble is also studied. In this talk, we show that the eigenvalue process of elliptic Ginibre ensemble satisfies the SDE which includes the above two models and discuss the relation between the behavior of the eigenvalues and normality of the matrix.
In this talk, we would like to consider infinite particle systems with jumps. Unlabeled systems (dynamical systems on the configuration space) are constructed by Esaki[Tohoku J, 2019] using Dirichlet form technique. Then, we would like to give infinite dimensional stochastic differential equation (ISDE) representations for each particle on the dynamics. However, the coordinate function can NOT be in the domain of the Dirichlet form associated with the unlabeled dynamics. Hence, we need to “label” for the unlabeled dynamics. After labelling, we can obtain ISDE representations for each particle. Under suitable conditions, our theorem can be applied to the systems of alpha-stable particles with logarithmic interactions associated with Dyson, Ginibre, Airy and Bessel random point fields, which are related to the random matrix theory. This is a joint work with Hideki Tanemura (Keio University).
The planner Gaussian analytic function (GAF) is an entire function defined on the complex plane such that the coefficients are Gaussian random variables. Let $\{ \xi _n\}$ be independent and identically distributed, and Gaussian random variables with mean free and unit variance. We take the nth coefficient of the entire function to be $\xi _n / \sqrt{n!} $. Then the zero points of the planner GAF are a translation and rotation invariant random point field on the complex plane. We call the random point field the planner GAF. We prove that the associated distorted Brownian motion (interacting Brownian motion) exists. We specify its labeled dynamics and present the explicit formula of the logarithmic derivative of the planner GAF. Applying the general theory, we obtain the solution of the infinite-dimensional stochastic differential equation thus obtained.
This is joint work with Subrho Ghosh and Tomoyuki Shirai.