�P�D���{���p�����w��
��N�A���{���p�����w��Ɍ�������u�܂莆�H�w�̐����v���������܂����B���{���p�����w��Ƃ͐��w�̉��p��H�w���̕���ŁA�v�Z�@�␔�w���D���Ȑl�B���W�܂���1990�N�ɔ��������w��ł���ƁA�M�҂͏���Ɏv���Ă��܂��B�č��̊w��SIAM�i�T�C�A���ASociety for Industrial and Applied Mathematics�j��ڕW�ɐݗ����ꂽ���߁AJSIAM�i�W���p���T�C�A���j�Ƃ��Ă��܂��B�ڂ����̓z�[���y�[�W
http://wwsoc.nii.ac.jp/jsiamw/�������������B
�Q�D�܂莆�H�w�̐���
2003�N�A�w����ɐ܂莆�H�w�Ɋւ��錤����g�D���ĂĂ�낤�ł͂Ȃ����Ƃ����b�������H�Ƒ�w�̔�����Y���𒆐S�Ɏ����オ��A��C���q�a�̎w���̂��ƁA��B��w�ŋ��{�Ȗځu�܂莆�̐����v��S�����Ă����M�҂���������̐ݗ��Ɋւ�荇�����ƂɂȂ�܂����B����̎�|�͎��̂Ƃ���ł��B�u���{��̐܂莆��Ori-gami�Ƃ��āA���⍑�ی�ƂȂ��Ă���B����̓A�[�g��z�r�[�Ƃ��Ă̒n�ʂ��m�ۂ����邱�Ƃ��Ӗ����Ă���B�������A�����ɍH�Ƃ̉��p�͖w�nj����Ȃ��B�����A���s��w�q��F���H�w��U�̌����҂ɂ��A����܂ł̕��ʐ܂ɑ��A�~���܂�̈�ʉ�������ꂽ���Ƃɂ��A��ɍH�w�ւ̉��p����������тт邱�ƂƂȂ����B�����ŁA�����Ɂu�܂莆�H�w�̐����v��������𗧂��グ�V���������̍\�z��ڎw���B�v
�����āA�ŏ��̌����W�2003�N3��20���ɓ����H�Ƒ�w�̑剪�R�L�����p�X�ŊJ����A�쓇���q���A�{�苻�A���q�a�ɉ����āA�C�O����̔�ѓ���u��������܂����B
�R�D���{���p�����w��N��
����̊������e��2003�N�H�ɋ��s��w�ŊJ�Â��ꂽ���{���p�����w��N��ɂ�����Z�b�V�����u�܂莆�̐����ƍH�w�v�ł��B15������30���̍u�����S����9������A���O��40�����x�Ɛ����ł����B�w����ǂ̕������ꂳ���ȂǁA�F�����ÁX�ƌ������ʎ����Ŏ����X���Ă����܂����B�܂莆�A�H�w�A���w�̌��т����V�N�ȋ����������Č}����ꂽ�悤�Ɏv���܂��B�u���҂ƍu����ڂ͎��̒ʂ�ł��B
���Ǝi��F������Y�i���H��j
�� �쓇���q�i����j�F�������ɂ��
�\�����f���i���H�w�̒�āj
�� ��仁i���H��A���{�����j�A�R�{��q�i�x�m�d�H�j�A������Y�i���H��j�F�������\���̍���
�� �{�苻��i����j�F�P���r���̗��̂�4�����ł����
�� ���c�_��i���Q��j�F���ʑ̂Ɨ��̐܂莆
�� ���G���FSome Mathematical Observation on Flat Conditions of Origami
�� ����ʍO�i�F���Ȋw���j�F�F���\�����H�w�Ɛ܂莆
�� �쓇���q�i����j�F�����Ɍ����闆���͗l��͂����܂��^�܂莆���f��
�� ���L���A���q�q���A������Y�i��
�H��j�F�����ނ̈����
�� ���������F3�p�`�ƂS�ʑ̂Ƃ̑��ݕϊ�
������S���������̂͑�ςȂ̂ŁA����͖{���ɂ҂�����̕��c���̔��\�ɓI���i���ĉ���������Ǝv���܂��B�܂��A���̌����Ŏg���Ă��铮�I�v��@�́A���҂̖{�Ƃł���œK���̕���ł悭�m��ꂽ��@�ł���Ƃ����_�����c����I���R��1�ł��B�L�����ƂɁA���c���̓z�[���y�[�W��Ɏ��������J���Ă����܂��Bhttp://www.ed.ehime-u.ac.jp/ �ڂ������Ƃ�m�肽�����͂�����Q�l�ɂ��ĉ������B�M�҂̂��̋L�������c���̍u���Ƙ_���ALubiw��O�fRourke�̘_������ɂ��Ă��܂��B
�S�DLatin Cross
�܂��A�}�P�������������B
�}�P
�u�}�P�̗p���������闧�͉̂����H�v�Ɩ����A���w���ł������͕�����܂��B����͗����̂ł��B�Ƃ��낪�A�u�ǂ̂悤�ɐ܂�������Ă��悯��A����ȊO�Ɋ������������B�v�Ƃ�������Lubiw��O�fRourke�����߂Ďw�E���܂����B����ɕ��c���͑S�Ă̓ʑ��ʑ̂���܂����B
�}�Q��������1�ł��B

�}2
���ۂɐ܂��Ă݂�Ε�����悤�ɁA�}�Q����o���オ��}�`�͎l�ʑ̂ł��B

�}3
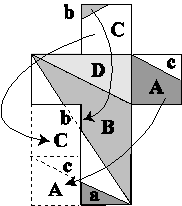
�iA�C���͐}4���Q�Ɓj�������A�܂��Ă݂Ȃ��Ƃ��A�}�Q�Ɉ�H�v��������A�l�ʑ̂̂����悻�̌`�͕�����܂��B���ꂪ�}4�ŁA�����������̔��\�Ƀq���g�č�}���Ă݂܂����B
�}4
�}4�ɂ����āA�����͐܂����\���A�����Z���̐}�`�i�Ⴆ�AA��a�j�͍ŏI�I�ɓ���̖ʂ��\�����܂��B�O�p�`D�͂���1�Ŏl�ʑ̂�1�̖ʂɂȂ�AA+a��D�ƍ����ȎO�p�`�̖ʂ��\�����܂��BB+���͕ʂ̎O�p�`���\�����A�c���4�̐}�`�����킳���āAB+b�ƍ����ȎO�p�`���\�����܂��B
����ȊO�ɂ��A�}5����ܖʑ́A�}6���甪�ʑ̂��ł�������܂��B
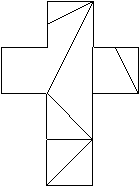
�}5

�}6
��l�͓W�J�}�Ƃ���17�ʂ�A�ʑ��ʑ�(�Ԃ�ĕ��R�ɂȂ������̂��܂�)�͍����Ȃ��̂�������5��ނ��邱�Ƃ������܂����B
�T�DLubiw��O�fRourke�̍l����
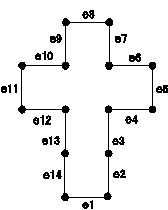
�}7
��l�͐悸�܂莆�̎��͂ɐ}7��14�{�̕Ӂiedge�j e1�A�c�Ae14 ��p�ӂ��A������\�荇�킹����@�𐔂��グ��悢�ƍl���܂����B
���������ƁA�u����͂������낤�B�v�Ǝv���l�����邩�Ǝv���܂����A����͌����Ď����ȃA�C�f�B�A�ł͂���܂���B�����܂ł��Ȃ��A�܂莆�ł͐܂��������ł��B�܂��������ׂɈꎞ�I��2�̕ӂ����킹�邱�Ƃ͕W���I�ł����Ă��A�d�オ��̍�i�ɂ����č��킹��ӂ̑g�ݍ��킹���ŏ��ɍl���邱�Ƃ͂߂����ɂȂ��Ǝv���܂��B
��l�͓\�荇�킹��ӂ̑g�ݍ��킹�����肵����A���ۂɐ܂邱�Ƃɂ��܂�����m�肳���܂����B
�����Ŗ��ɂȂ�͕̂ӂ̑g�������悭���߂���@�ł��B�Ⴆ�A�}8�ōŏ���e8��e13��\�荇�킹�邱�Ƃ����߂��Ƃ��܂��B

�}8
����Ǝ���e8��e13�ŕ��������2�̃O���[�v {e14�Ae1�Ae2�A�c�Ae7} �� {e9�Ae10�Ae11�Ae12} �̂��ꂼ��ŕӂ̑g�ݍ��킹�����߂�悢���ƂɂȂ�܂��B�����A�Ⴄ�O���[�v�ɑ�����2�ӁA�Ⴆ�� e5��e11 ��\�荇�킹�悤�Ƃ���ƁA���̑тō�����ւ�2�q�����悤�Ȍ`�ɂȂ��Ă��܂��A�ʑ��ʑ̂ł͂Ȃ��Ȃ�܂��B
���āA2�̕������͓����̖����ӂ̐������Ȃ��̂ʼn����Ղ��͂��ł��B���ꂼ��̃O���[�v���ŐV���Ȃ̕ӂ̃y�A�[�����߂�A����ɏ����ȃT�C�Y��2�̕�����肪�����܂��B���̍�Ƃ��J��Ԃ��ƁA�S�Ă̕ӂ̓\�荇�킹���肪���܂�܂��B
�Ƃ��낪�A�ŏ���2�ӂ̑g�ݍ��킹�╔�����ɂ�����ŏ���2�ӂ̑g�ݍ��킹�ɂ���ẮA��X�s���l�܂��Ă��܂����Ƃ�����܂��B����͎���2�̏ꍇ�ł��B
�@ �������̕ӂ̐�����ł���B
�A �P�̒��_�̎���ɏW�܂�ʂ̓��p�̘a��360�x����D
�@�͖��炩�ł��B��{�̕ӂ̊ԂŃy�A�[����낤�Ƃ���ƁA�ӂ�1�{�]���Ă��܂��܂��B
�A�ɂ��ẮA�Ⴆ�Η����̂ł́A1�̒��_�̎���ɐ����`��3�W�܂��Ă���̂œ��p�̘a��90�x��3�{�A
270�x�ɂȂ�܂��B�������A����1�̒��_�̎���ɐ����`�̊p��5�ȏ�W�܂�ƁA���p�̘a��360�x���Ă��܂��܂��B�]���āA���̒��_�͌E�݁A�ʑ��ʑ̂ɂ͂Ȃ�܂���i�}9�j�B
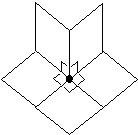
�}9
�܂�C�V�����ӂ̃y�A�[�����܂�x�ɁA���̕ӂ̗��[�̒��_�ɏW�܂�ʂ̐��������A���̌��ʁA�ʂ̓��p�̘a�������܂��B�����ŁA�\�荇�킹�钸�_�̃y�A�[���ɁC����������p�̘a���o���Ă����A���ꂪ360�x����ƁA���̕ӂ̑g�ݍ��킹�͕������܂��B
�@�A�̂ӂ邢�������邱�Ƃɂ��A�����݂��S���Ȃ��ӂ̃y�A�[�����X�ɔr�����邱�Ƃ��ł��܂��B����͓��I�v��@�A���}����@�̊�{�I�ȍl�����ł��B��l�͂��̎�@�ɂ��A�ӂ�e1�A�c�Ae14�Ɛݒ肵���Ƃ��A�W�J�}�Ƃ���17�ʂ�A�ʑ��ʑ̂�5��ނ��邱�Ƃ������܂����B
�U�D���c���ɂ�鐸����
���c���́A�}10�̂悤�ɕӂ������ƍׂ�����������A����ɑ����̓ʑ��ʑ̂���邱�Ƃ��o���邱�Ƃ������A�܂��A������ׂ����������Ă��W�J�}��85�ʂ�A�ʑ��ʑ̂�23�ʂ肵���Ȃ����Ƃ𖾂炩�ɂ��܂����B

�}10
���c����Latin Cross�ȊO�ɂ��A���^�A�ʌ^�A���^�Ȃǂ̗l�X�ȑ��p�`�ɂ��ē��l�̍l�@�������Ȃ��Ă��܂��B���ɁA�����`�ɂ��ďڂ����A�����`���疳���̓ʑ��ʑ̂���邱�Ƃ��ł��邱�Ƃ������܂����B
���c���̂��b�ɂ��A�p���̌`���ς���Ă��A�ӂ̑g�ݍ��킹�̗͌v�Z�@�łł��܂����A���ۂɑ��ʑ̂��\�������Ƃ͌v�Z�@�ł͎����ł��Ă��Ȃ������ł��B
�܂��A���Ƃő��ʑ̂�����Ă݂Ă��A���ꂪ���ʑ̂Ȃ̂������������ł͕������ꍇ������܂��B�Ⴆ�A�}11�̂悤�ȋ�ԓ��̎l�ӌ`ABCD�����R�Ȃ̂��A����Ƃ�BD�ɐ܂�ڂ����Ă���̂��͌v�Z���Ă݂Ȃ���Δ���ł��܂���B���ׂ̈ɂ́A���_A�AC�̋�ԍ��W�����߂��̂��A��ԓ��ł�AC�̒��������ƌ��̗p���ɂ�����2�_�Ԃ̋������ׂ�̂����܂���ł��B��������Ε��R�ŁA��ԓ��̒��������̕����Z����ΐ܂�ڂ����Ă��܂��B�i����͎��̃[�~��4�N���A���G���q���C�t���܂����B���݂ɁA�M�҂��v�������̂ͤ�x�N�g����p������@�ł����B�j
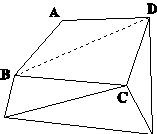
�}11
���c���͈��Q��w����w���Ō������s���Ă����܂����C���܂��܂ȃ��x���̋���ł��̑�ނ����Ă�����Ǝf���܂����B��w�ڂ�������͕��c���ɂ��肢����̂��悢���Ǝv���܂��D
�Q�l����
[1] ���c�_��u�W�J�}�Ƒ��ʑ́v���Q�������w�Z���猤����w���, 40, 14—18 (1999).
[2] A. Lubiw and J. O�fRourke, �gWhen can a polygon fold to a polytope?�h,
Technical Report 048, Dept. Comput. Sci.,
[3] J. O�fRourke, Folding and Unfolding in
Computational Geometry, Proc.