Kernels for Langlands' Transfer and Non-linear Poisson Formulas

Prof. L.Lafforgue (IHES)
QuickTime, 55m24s
Classical spectral decomposition, both local and global, are introduced. In particular, when applied to the general linear group $GL_r$, this leads to the local and global $L$ and $\varepsilon$-factors, once we enlarge the base space from $GL_r$ to $M_r$, the space of $r\times r$-matrices.
Recorded from 10:10am of April 26, 2013, this is the first talk given at the symposium on 'Automorphic Functions and Arithmetic Geometry', held at the Graduate School of Mathematics, Kyushu University, Fukuoka, Japan.
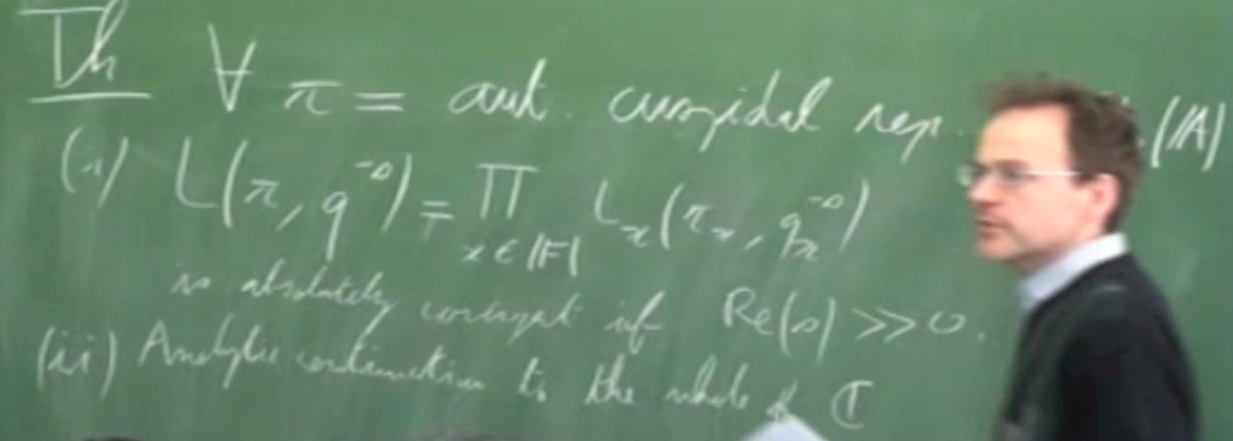
Prof. L.Lafforgue (IHES)
QuickTime, 54m05s
Local and global $L$ and $\varepsilon$-factors are introduced and their standard properties are summarized. The results are classical, but the way they are presented here is original.
Recorded from 11:10am of April 26, 2013, this is the 2th talk given at the symposium on 'Automorphic Functions and Arithmetic Geometry', held at the Graduate School of Mathematics, Kyushu University, Fukuoka, Japan.
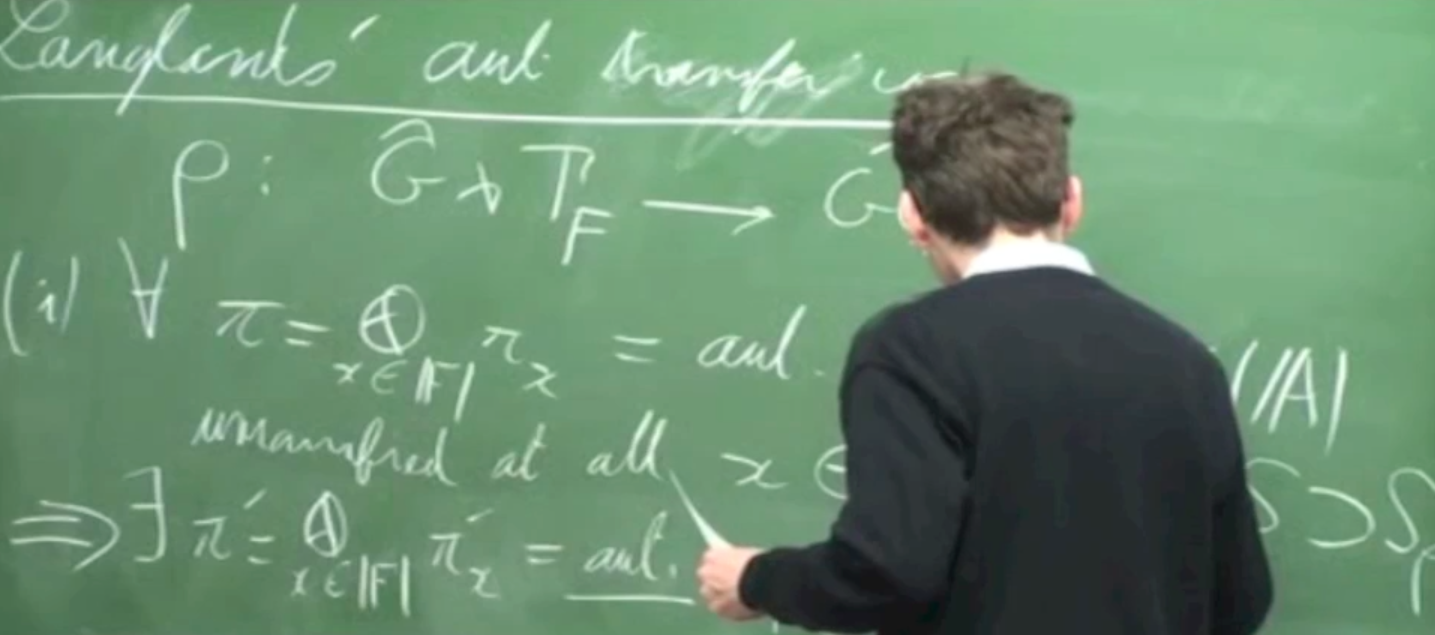
Prof. L.Lafforgue (IHES)
QuickTime, 1h00m57s
Langlands' automorphic transfer conjecture and its consequences are presented. The transfer rules by a transfer representation $\rho$ proposed by Langlands lead to the definition of non linear $L$-functions, whose global propoerties are deduced from the automorphic transfer conjecture.
Recorded from 10:10am of April 27, 2013, this is the 3th talk given at the symposium on 'Automorphic Functions and Arithmetic Geometry', held at the Graduate School of Mathematics, Kyushu University, Fukuoka, Japan.
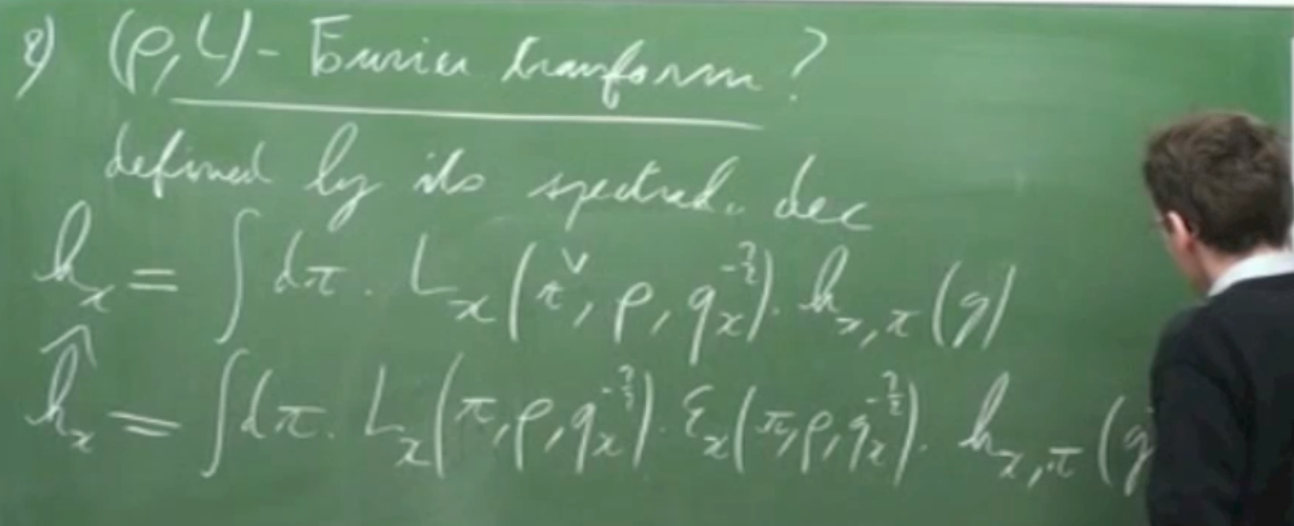
Prof. L.Lafforgue (IHES)
QuickTime, 59m42s
New types of function spaces and of $(\rho,L)$-Fourier transforms on these spaces are associated to transfer representations $\rho$, through local spectral decomposition. Non-linear Poisson formulas without boundary terms are presented and are deduced from Langlands' automorphic transfer conjecture.
Recorded from 11:10am of April 27, 2013, this is the 4th talk given at the symposium on 'Automorphic Functions and Arithmetic Geometry', held at the Graduate School of Mathematics, Kyushu University, Fukuoka, Japan.
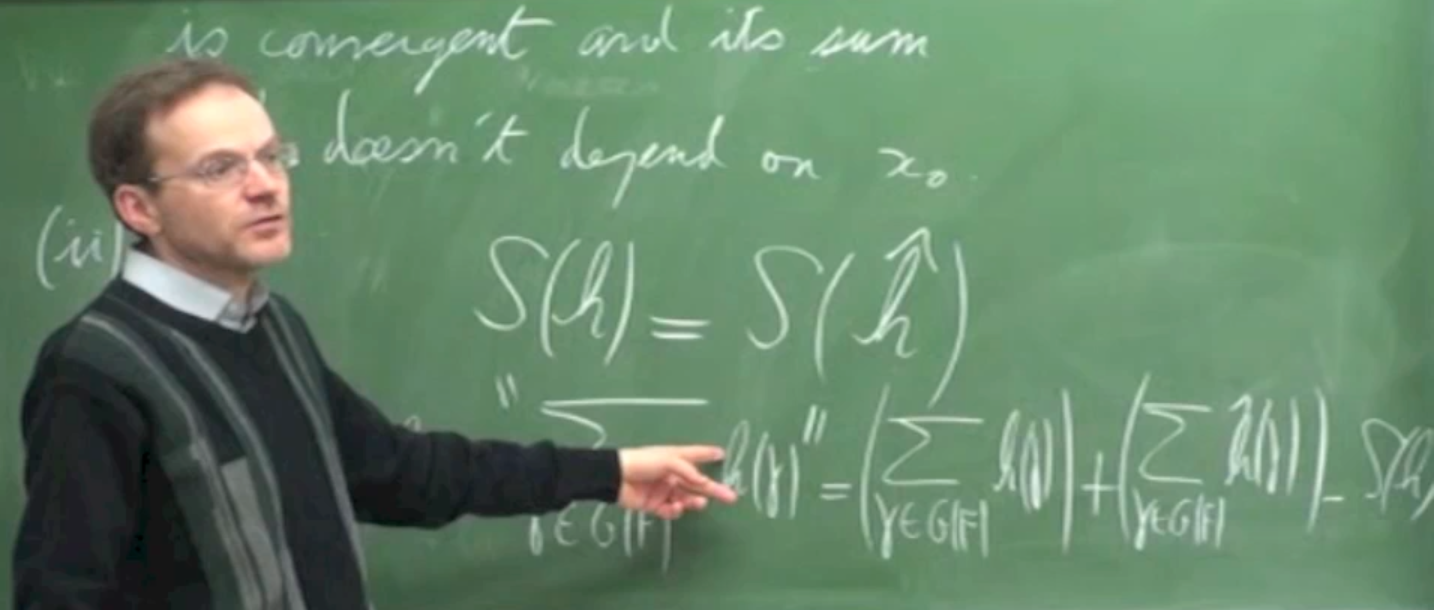
Prof. L.Lafforgue (IHES)
QuickTime, 43m56s
The non-linear Poisson formulas without boundary terms introduced in the previous lecture are conjecturally generalised to non-linear Poisson formulas with boundary terms.
Recorded from 10:10am of April 28, 2013, this is the 5th talk given at the symposium on 'Automorphic Functions and Arithmetic Geometry', held at the Graduate School of Mathematics, Kyushu University, Fukuoka, Japan.

Prof. L.Lafforgue (IHES)
QuickTime, 1h16m45s
The notion of 'kernels' of Langlands' automorphic tranfer is introduced. As an application, Langlands' automorphic tranfer conjecture is deduced from the non-linear Poisson formulas.
Recorded from 11:00am of April 28, 2013, this is the last talk given at the symposium on 'Automorphic Functions and Arithmetic Geometry', held at the Graduate School of Mathematics, Kyushu University, Fukuoka, Japan.
